● タンパク質間ドッキング予測精度
ZLAB docking benchmark 4.0 (
Mintseris et al., Proteins 2010) を用いたタンパク質ドッキングの精度 (Success Rate) を示します.Success Rateは,横軸に候補構造の出力数 \(N\) をとり,ドッキング予測で上位 \(N\) 位以内に正解構造に近い構造 (near native) が存在した場合にその複合体の予測に成功 (Success) したとし,成功した複合体の割合を176個の複合体で求めたものです.正解構造に近い構造 (near native) の基準は,\( \mbox{Ligand-RMSD}< 5 \mathrm{\unicode{x212B}} \) としています.\(\mbox{Ligand-RMSD}\)はレセプタータンパク質(
-Rオプションで指定したPDB) を重ね合わせたときのリガンドタンパク質のRMSD値として求められます.Success RateはZDOCK 2.3 (
Chen et al., Proteins, 52(1): 2003.) および,ZDOCK 3.0 (
Mintseris et al., Proteins, 69(3): 2007.) と比較をしました.
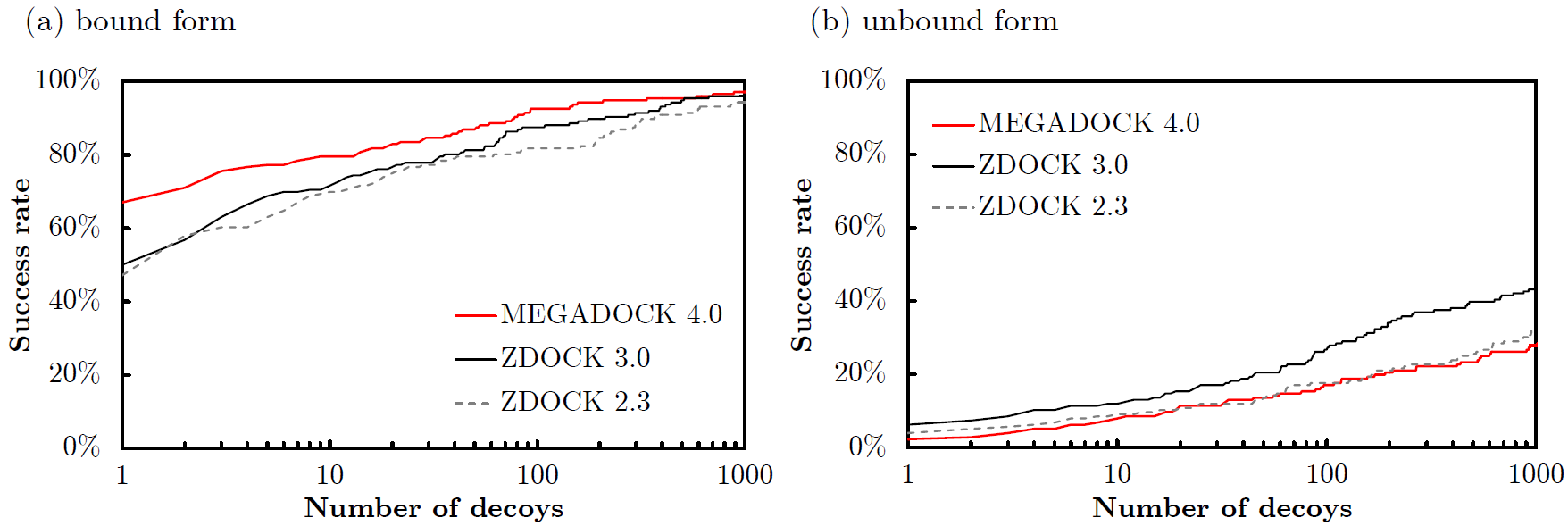
図:ZLAB docking benchmark 4.0の176複合体のドッキング予測精度.
● タンパク質ドッキング予測の計算時間(1 CPUコア)
ZLAB Docking Benchmark 4.0の352 (bound/unbound 両方) 複合体のドッキング計算にかかったトータルの時間と1ペアの平均計算時間を以下の表に示します.計算にはMEGADOCK, ZDOCKともにIntel Xeon X5670 CPU (Westmere-EP, 2.93GHz, 6 cores) の1コアを使用しています.MEGADOCK 4.0のバイナリ
megadockとFFTW3ライブラリはIntel C++ Compiler version 14.0.2.144を用いてコンパイルしています.
表:ZLAB Docking Benchmark 4.0 (352複合体) の計算時間
|
|
MEGADOCK 4.0
|
ZDOCK 2.3
|
ZDOCK 3.0
|
|
Total (352 docking) time (hour)
|
67.1
|
309.2
|
684.3
|
|
Averaged (1 docking) time (min)
|
11.4
|
52.7
|
116.6
|
|
Speedup from ZDOCK 3.0
|
10.20
|
2.21
|
(1.0)
|
● GPUを用いたときの計算時間
GPUによる演算加速 MEGADOCK 4.0でGPUを用いた時の計算時間を示します.使用したバイナリ
megadock-gpuはCUDA 6.0とIntel C++ Compiler version 14.0.2.144を用いてコンパイルしています.計算にはIntel Xeon X5670 CPU (Westmere-EP, 2.93GHz, 6 cores) を2ソケット (12 CPU cores), およびNVIDIA Tesla K20X (GK110) GPUを3枚搭載したノードを用いています.
表:ZLAB Docking Benchmark 4.0 (352複合体) の計算時間.12CPUコア利用時は,24スレッド指定(hyper threading)を使用しています.
|
|
1 CPU core
|
12 CPU cores
|
12 CPU cores & 1 GPU
|
12 CPU cores & 3 GPUs
|
|
Total (352 docking) time (hour)
|
67.1
|
8.20
|
2.26
|
1.02
|
|
Averaged (1 docking) time (min)
|
11.44
|
1.40
|
0.39
|
0.17
|
|
Speedup from 1 CPU core
|
(1.0)
|
8.1
|
29.7
|
65.8
|
CUDAのバージョンによる速度の比較 また,GPUを用いてMEGADOCK 4.0を実行する際に,CUDAのバージョンによって計算速度が変化します.CUDA 5.0~7.5について測定した結果を以下に示します.以下のデータは,ZLAB Docking Benchmark 5.0 bound conformation (230複合体) の計算時間を測定したものです.Intel Xeon X5670 CPU (Westmere-EP, 2.93GHz, 6 cores) を2ソケット (12 CPU cores), およびNVIDIA Tesla K20X (GK110) GPUを3枚搭載したノードを用いて,1 CPU core + 1 GPU時,および12 CPU cores (24 Hyper thread) + 3 GPUs時の測定を行いました.
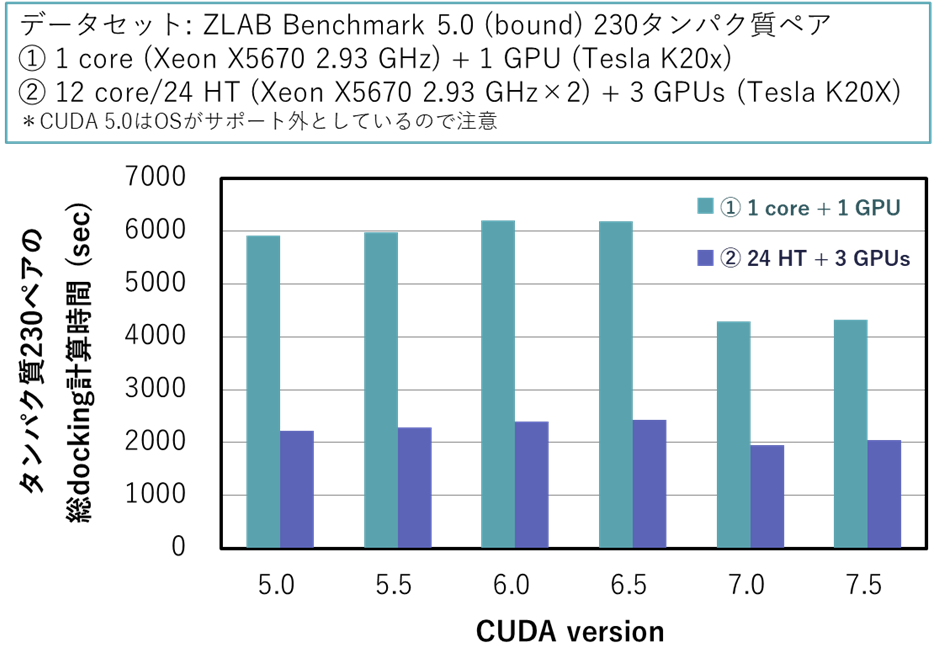
図:CUDAのバージョンごとのMEGADOCK (GPU版) 計算時間
● GPUスーパーコンピュータを用いたときの計算時間
MEGADOCK 4.0でGPUスーパーコンピュータを用いた時の計算時間と並列化効率を示します.使用したバイナリ
megadock-gpu-dpはCUDA 6.0とIntel C++ Compiler version 14.0.2.144, OpenMPI version 1.6.5を用いてコンパイルしています.計算には東京工業大学 学術国際情報センターのTSUBAME 2.5のThinノードを用いています.Thinノードは2ソケットのIntel Xeon X5670 CPU (2.93GHz, 6 cores) と3枚のNVIDIA Tesla K20X (GK110) GPUを搭載しています.ハードウェアの詳細に関しては
東京工業大学 学術国際情報センターのHPをご覧ください.
表:ノード並列時の計算時間と並列化効率(強スケーリング).計算時間はZLAB Benchmarkの176複合体のbound/unboundの両方を全て計算した352回の計算の積算です.
|
#Nodes \(n\)
|
35
|
70
|
105
|
140
|
210
|
280
|
350
|
420
|
|
#CPU cores
|
420
|
840
|
1,260
|
1,680
|
2,520
|
3,360
|
4,200
|
5,040
|
|
#GPUs
|
105
|
210
|
315
|
420
|
630
|
840
|
1,050
|
1,260
|
|
Time \(T_n\) (min)
|
264.4
|
133.3
|
90.6
|
67.4
|
44.6
|
33.1
|
26.7
|
22.5
|
|
\(\mbox{Strong Scaling}_n\)*
|
-
|
0.991
|
0.973
|
0.981
|
0.988
|
0.997
|
0.990
|
0.980
|
| * \(\mbox{Strong Scaling}_n = (T_{35}/T_n) / (n / 35)\) |
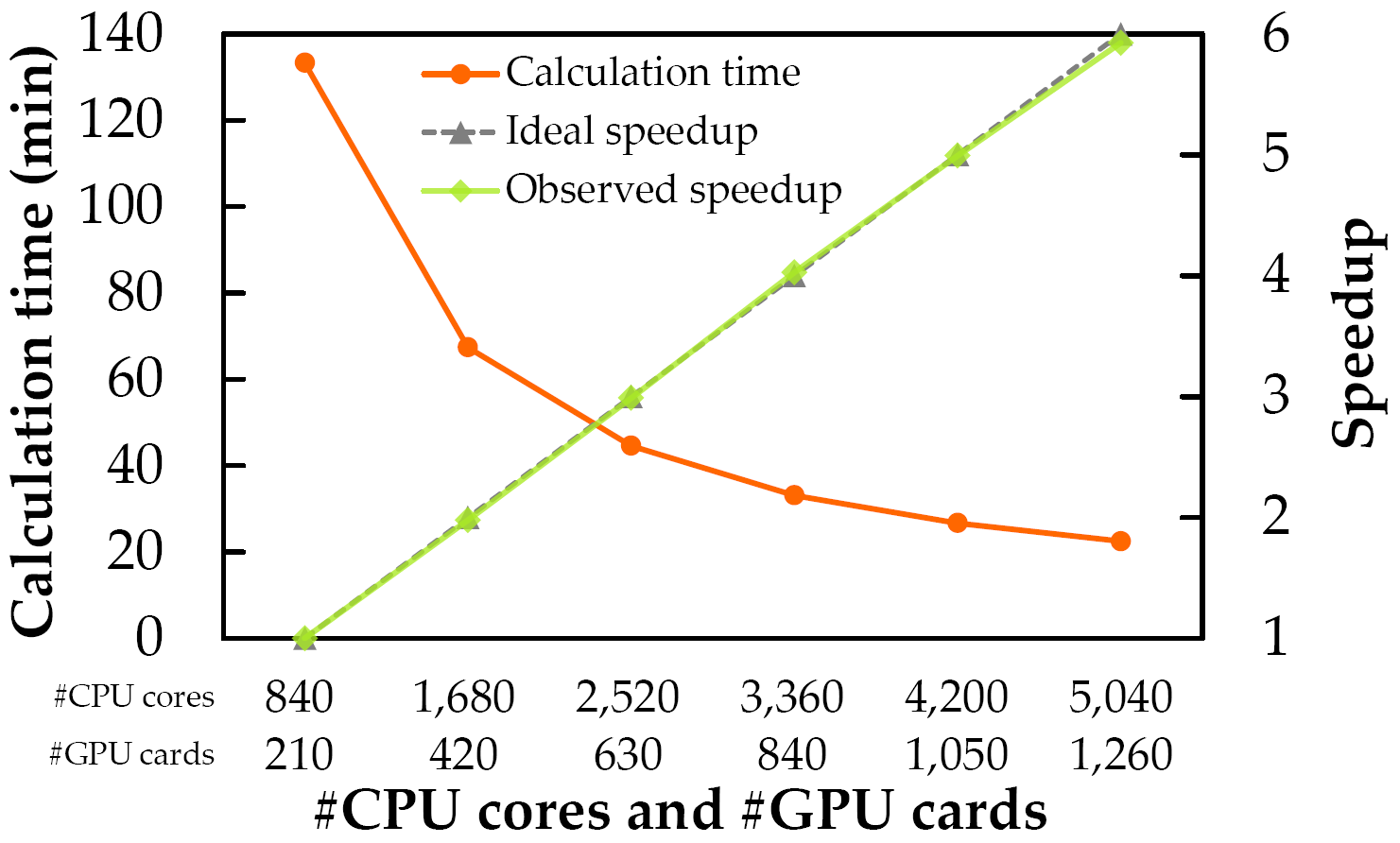
図:ノード並列時の計算時間と並列化効率(強スケーリング)
● MEGADOCKのドッキングスコア関数
MEGADOCK 4.0は,タンパク質ドッキング予測で最もよく用いられている「3次元グリッド上の高速フーリエ変換 (FFT) による方法 (Katchalski Algorithm)」を用いています (
Katchalski-Katzir et al., Proc Natl Acad Sci USA, 89(6): 1992.).Katchalski Algorithmではタンパク質の構造情報を3次元グリッド上で表し,2つのタンパク質で作られる複合体候補構造の評価値 \(S(\alpha, \beta, \gamma)\) を,離散フーリエ変換 (DFT) と逆離散フーリエ変換 (IDFT) による離散フーリエ空間上の相関関数によって計算します.
\begin{align*}
S(\alpha, \beta, \gamma) &= \sum_{l=1}^N \sum_{m=1}^N \sum_{n=1}^N R(l,m,n)L(l+\alpha, m+\beta, n+\gamma)\\
&= \mathrm{IDFT}[\mathrm{DFT}[R(l,m,n)]^* \mathrm{DFT}[L(l,m,n)]]
\end{align*}
ここで,\(R\) と \(L\) はレセプタータンパク質 (\(R\)) とリガンドタンパク質 (\(L\)) のグリッド上での離散関数,\((l, m, n)\) は3次元グリッドの各座標点,\((\alpha, \beta, \gamma)\) はリガンドタンパク質の並進移動ベクトルです.アスタリスクの演算子 \(*\) は複素共役を表します.\(S(\alpha, \beta, \gamma)\) の相関関数(畳み込み和)を直接計算すると \(\mathcal{O}(N^6)\) の計算量が必要となりますが,高速フーリエ変換 (FFT) によってDFTとIDFTを計算することで計算量は \(\mathcal{O}(N^3 \log N)\) に削減されます.なお,MEGADOCKではこの \(S(\alpha, \beta, \gamma)\) の計算をリガンドタンパク質を回転させながら,その角度ごとに逐一計算します.デフォルトでは15°刻み(3,600通り),
-Dオプション利用時では6°刻み(54,000通り)の回転パターンでそれぞれ計算します.候補構造は,各角度ごとに最良の評価値(
-tオプション利用時は各角度ごとに上位 \(t\) 個)となる \((\alpha, \beta, \gamma)\) の位置が,評価値の良い順に
-N個(デフォルトでは2,000個)出力されます.
離散関数 \(R\) と \(L\) は,通常複数の物理化学的効果を考慮します.代表的なものは,ZDOCK (
Pierce et al., PLOS ONE, 6(9): 2011.) やPIPER (
Kozakov et al., Proteins, 65(2): 2006.),SDOCK (
Zhang et al., J Comput Chem, 32(12): 2011.) のような,形状相補性と静電相互作用,脱溶媒和自由エネルギーの3つの効果を評価関数として利用したものです.例えばこれら3つの効果を用いる場合は,以下のように評価関数を各評価関数の重み付き和とします.
\begin{align*}
S_{\mathrm{total}}&= w_{\mathrm{shape}}S_{\mathrm{shape}}+w_{\mathrm{elec}}S_{\mathrm{elec}}+w_{\mathrm{desol}}S_{\mathrm{desol}}\\
S_{\mathrm{shape}}&= \mathrm{IDFT}[\mathrm{DFT}[R_{\mathrm{shape}}(l,m,n)]^* \mathrm{DFT}[L_{\mathrm{shape}}(l,m,n)]]\\
S_{\mathrm{elec}}&= \mathrm{IDFT}[\mathrm{DFT}[R_{\mathrm{elec}}(l,m,n)]^* \mathrm{DFT}[L_{\mathrm{elec}}(l,m,n)]]\\
S_{\mathrm{desol}}&= \mathrm{IDFT}[\mathrm{DFT}[R_{\mathrm{desol}}(l,m,n)]^* \mathrm{DFT}[L_{\mathrm{desol}}(l,m,n)]]
\end{align*}
この例では,最終的な評価関数が3回の畳み込み和で計算されます.実際には,脱溶媒和自由エネルギー \(S_{\mathrm{desol}}\) に複数回の畳み込み和を費やすことが多く,例えばZDOCKでは6回,PIPERでは9回の畳み込み和を \(S_{\mathrm{desol}}\) の計算に使います.
一方MEGADOCKでは,ZDOCK等と同様に形状相補性・静電相互作用・脱溶媒和自由エネルギーを取り入れていますが,畳み込み和は1回のみ用いて計算を行います.独自の形状相補性評価関数rPSC (\(S_{\mathrm{rPSC}}\)) と脱溶媒和自由エネルギー評価関数 (\(S_{\mathrm{RDE}}\)) によって1回のみの畳み込み和による3効果同時計算を以下のように行っています.
\begin{align*}
S_{\mathrm{total}}&= \Re \left[\mathrm{IDFT}[\mathrm{DFT}[R(l,m,n)]^* \mathrm{DFT}[L(l,m,n)]] \right]\\
R(l,m,n) &= R_{\mathrm{rPSC}}(l,m,n) + w_{\mathrm{RDE}}R_{\mathrm{RDE}}(l,m,n) + iR_{\mathrm{elec}}(l,m,n)\\
L(l,m,n) &= L_{\mathrm{rPSC\&RDE}}(l,m,n) -iw_{\mathrm{elec}} L_{\mathrm{elec}}(l,m,n)
\end{align*}
MEGADOCKのより詳しい情報については,以下の文献や参考文献リストを参照下さい (
Ohue et al., Lecture Notes Comput Sci, 7632: 2012.;
Ohue, Ph.D. Thesis, Tokyo Institute of Technology, 2014.).
● 参考文献
- MEGADOCK評価関数(rPSC形状相補性項)
Ohue M, et al., MEGADOCK: An all-to-all protein-protein interaction prediction system using tertiary structure data, Protein Pept Lett, 21(8): 766-778, 2014.
- MEGADOCK評価関数(RDE脱溶媒和項)
Ohue M, et al., Improvement of the Protein-Protein Docking Prediction by Introducing a Simple Hydrophobic Interaction Model:
an Application to Interaction Pathway Analysis, Lecture Notes in Comput Sci, 7632: 178-187, 2012.
- MEGADOCK for CPU supercomputer (MEGADOCK 3.0/MEGADOCK-K)
Matsuzaki Y, et al., MEGADOCK 3.0: A high-performance protein-protein interaction prediction software using hybrid parallel computing for petascale supercomputing environments, Source Code for Biol Med, 8(1): 18, 2013.
- MEGADOCK-GPU
Shimoda T, et al., MEGADOCK-GPU: Acceleration of Protein-Protein Docking Calculation on GPUs, In Proc of ACM-BCB 2013, 884-890, 2013.
- MEGADOCK for GPU supercomputer (MEGADOCK 4.0)
Ohue M, et al., MEGADOCK 4.0: an ultra–high-performance protein–protein docking software for heterogeneous supercomputers, Bioinformatics, 30(22): 3281-3283, 2014.
- MEGADOCK for Xeon Phi
Shimoda T, et al., Protein-Protein Docking on Hardware Accelerators: Comparison of GPU and MIC Architectures, BMC Systems Biology, 9(S1): S6, 2015.





 Copyright © 2014-2019 Akiyama Laboratory, Tokyo Institute of Technology, All Rights Reserved.
Copyright © 2014-2019 Akiyama Laboratory, Tokyo Institute of Technology, All Rights Reserved.