an ultra-high-performance protein-protein docking for heterogeneous supercomputers

Application to Protein-Protein Interaction Predictions

coming soon...


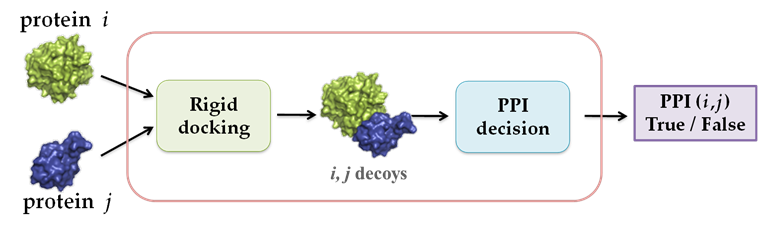
MEGADOCKはドッキング計算結果に基いてタンパク質間相互作用(PPI)予測（結合パートナー予測）を行うことができます． Matsuzaki et al., Protein Pept Lett 2014やOhue et al., BMC Proceedings 2013などでMEGADOCKによるタンパク質間相互作用予測 が行われており，網羅的な相互作用予測の結果からPPIネットワークを構築しています．

本頁ではPPI予測の手順について記載します．具体的なパスウェイ解析への応用例等については文献を参照して下さい．

● PPI予測（結合パートナー予測）の手順

PPI (Protein-Protein Interaction) 予測は，MEGADOCKに同梱しているppiscoreツールを用いて行います．ppiscoreにドッキ ングoutファイルと候補構造数を入力することで，PPI評価値 \(E\) を計算します．（ppiscoreはperlスクリプトで記述されています．）

1. MEGADOCKによる \(t=3\) ドッキング
まずMEGADOCKによって，相互作用の有無を予測したい対象の2つのPDBのドッキング計算を行います．このとき，-tオプションを3に，-Nオプションを10800に設定して下さい．

$ megadock -R rec.pdb -L lig.pdb -o dock.out -t 3 -N 10800

2. リランキングによる高精度化（省略可）
候補構造に対する詳細計算を行うツール（リランキングツール）を用いて高精度化を行います．ここではZRANK1 (Pierce et al., Proteins 2007) を用いてリランキングを行う手順を示します．

(1) PDBファイルに水素を付加する
ZRANKの計算には水素が付加されたPDBファイルが必要です．ここではReduceというフリーソフトを用いて水素付加を行う手順を示しますが，AmberのprotonateやDiscovery Studioなどでも同様の操作が可能です．

$ ./reduce rec.pdb > rec.pdb.h
$ ./reduce lig.pdb > lig.pdb.h 

(2) .outファイルを編集する
ドッキング出力ファイルの3行目と4行目にあるPDBファイル名を，水素を付けたPDBファイルに変更します．（(1)で上書きを行った場合は変更する必要はありません）

(3) ZRANKの実行
以下のようにZRANKを実行します．

$ ./zrank dock.out 1 10800

すると，dock.out.zr.outというファイルが生成されます．

3. PPI評価値の計算と評価
ppiscoreツールを使ってPPI評価値 \(E\) を計算します．

(a) リランキングを行わない（2. を省略した）場合

$ ./ppiscore dock.out 10800

(b) リランキングを行った場合

$ ./ppiscore dock.out 10800 dock.out.zr.out

※ZRANK以外のリランキングツールを利用する場合，ツールの出力に沿って.outファイルの中身をソートしておくことで，(a)の手順で計算可 能です．

計算したPPI評価値 \(E\) に対して閾値 \(E^*\) を定め，\(E^*\) との値の大小でPPIの有無を判定します． \begin{align*} \begin{cases} E > E^* & → 相互作用する\\ E \leq E^* & → 相互作用しない \end{cases} \end{align*} 感度 (sensitivity, recall) と選択度 (precision) のトレードオフになりますが，通常は \(E^*=6.0～7.0\) 程度に設定します．選択度を高くしたいと きは \(E^*=10.0～13.0\) 程度に上げます．\(E^*\) による精度の変化についてはZLAB docking benchmark (Mintseris et al., Proteins 2010) の複合体を用いて検証した結果を下部に載せましたのでそちらもご覧ください．

● PPI予測の性能情報（ZLAB Docking Benchmarkを用いた検証）

ZLAB docking benchmark 4.0の120個の複合体の結合相手を全通りで入れ替えて（14400個の）PPI評価値 \(E\) を計算し，正しい結合相手を識別できるか検証した結果を示します．用いた120個の複合体のPDB ID (BenchmarkのIDに準拠) を以下の表に示します．

表：PPI予測に用いた120複合体のPDB IDリスト (ZLAB docking benchmark 4.0 より)

Rigid-body (79)
1AK4, 1AVX, 1AY7, 1B6C, 1BUH, 1BVN, 1CGI, 1CLV, 1D6R, 1DFJ, 1E6E, 1E96, 1EAW, 1EFN, 1EWY, 1F34, 1FC2, 1FFW, 1FLE, 1FQJ, 1GCQ, 1GHQ, 1GL1, 1GLA, 1GPW, 1GXD, 1H9D, 1HE1, 1J2J, 1JTG, 1KAC, 1KTZ, 1KXP, 1KXQ, 1MAH, 1N8O, 1OC0, 1OPH, 1OYV, 1PPE, 1PVH, 1QA9, 1R0R, 1S1Q, 1SBB, 1T6B, 1TMQ, 1UDI, 1US7, 1XD3, 1YVB, 1Z0K, 1Z5Y, 1ZHH, 1ZHI, 2A5T, 2A9K, 2ABZ, 2AJF, 2B42, 2BTF, 2FJU, 2G77, 2HLE, 2HQS, 2I25, 2J0T, 2O8V, 2OOB, 2OUL, 2PCC, 2SIC, 2SNI, 2UUY, 2VDB, 3D5S, 3SGQ, 7CEI, BOYV
Medium Difficulty (23)
1ACB, 1GRN, 1HE8, 1I2M, 1JIW, 1LFD, 1M10, 1MQ8, 1NW9, 1R6Q, 1SYX, 1WQ1, 1XQS, 2AYO, 2CFH, 2H7V, 2HRK, 2J7P, 2NZ8, 2OZA, 2Z0E, 3CPH, 4CPA
Difficult (18)
1ATN, 1BKD, 1F6M, 1FQ1, 1H1V, 1IBR, 1IRA, 1JK9, 1PXV, 1R8S, 1Y64, 1ZLI, 1ZM4, 2C0L, 2I9B, 2IDO, 2O3B, 2OT3

もともとの複合体の結合相手を正解とし，評価値 \(E\) と閾値 \(E^*\) に基いてPPI予測を行ったときの精度を示します．相互作用すると予測したペアが正しい複合体である場合をTrue Positive (TP)，相互作用すると予測したペアが正しい複合体でない場合をFalse Positive (FP)，相互作用しないと予測したペアが正しい複合体である場合をFalse Negative (FN)，相互作用しないと予測したペアが正しい複合体でない場合をTrue Negative (TN)，とし，TP, FP, FN, TNのペア数から以下の式で各精度の値を計算します． \begin{align*} \mathrm{Precision}&=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}\\ \mathrm{Sensitivity\ (Recall)}&=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}\\ \mathrm{F}\mbox{-}\mathrm{measure\ (F_1}\mbox{-}\mathrm{score)}&=\frac{2\cdot\mathrm{TP}}{2\cdot\mathrm{TP}+\mathrm{FP}+\mathrm{FN}} \end{align*} 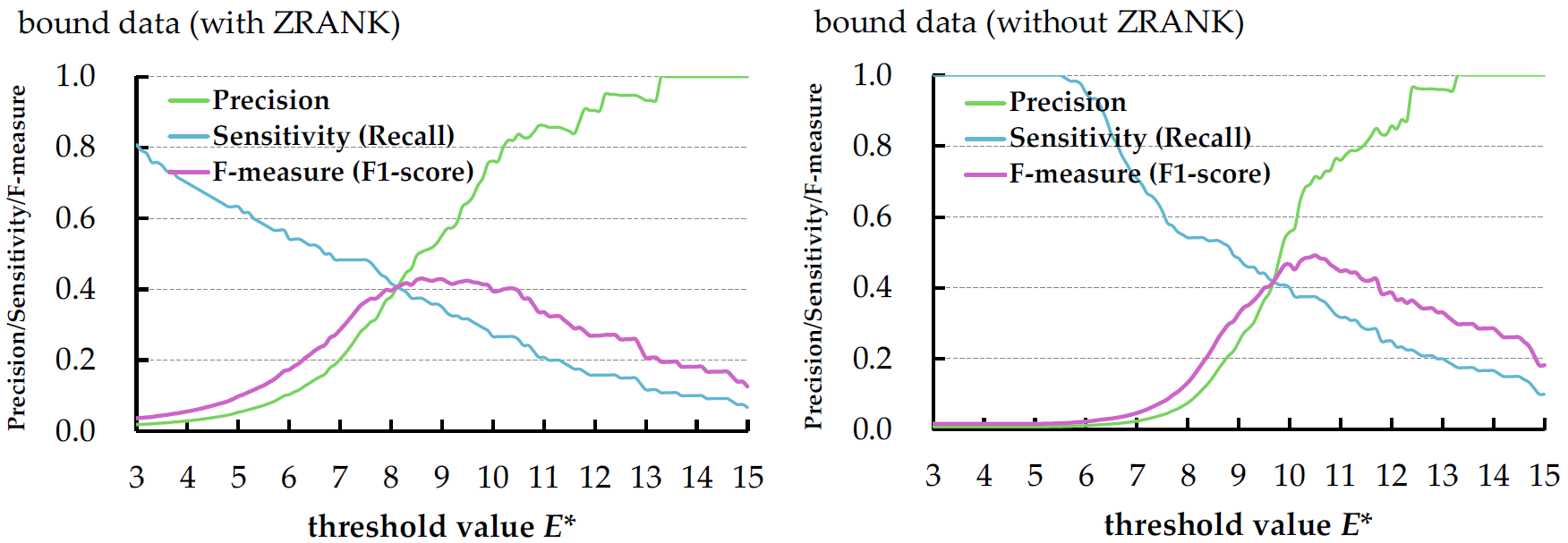それぞれの精度の閾値 \(E^*\) による変化を下図に示します．左はリランキングを行ったもの，右はリランキングを行わない場合のものです．両者ともbenchmarkのboundデータを使用しています．


また，あるレセプタータンパク質から見たときの120個のリガンドタンパク質のPPI評価値の順位から，「正しい相手がどのくらい上位にいるか」(early recognition problemと呼ばれます) を評価するいくつかの指標を計算し，120個のレセプタータンパク質で平均をとったものを以下の表に示します．各値の説明 は表の下に記述します．

	bound 120x120 (with ZRANK)	bound 120x120 (without ZRANK)	unbound 120x120 (with ZRANK)	unbound 120x120 (without ZRANK)
ARP	20.05	21.66	60.67	54.97
RIE	4.661	4.832	0.988	1.165
AU-ROC	0.840	0.826	0.499	0.546
AU-AC	0.833	0.820	0.494	0.542
BEDROC	0.602	0.624	0.127	0.150
EF	3.458	3.625	0.958	1.167
※これらの値は120個のレセプタータンパク質について計算したものを平均したものになります．

• ARP: Average Rank of Positives. 正しい相手の順位の平均値．小さいほど良い値．今回は正しい相手は1つのみなので，単純に順位の値となります．
• RIE: Robust Initial Enhancement. 大きいほど良い値．以下の式で計算されます． \[ \mathrm{RIE}=\displaystyle\frac{\sum_{i=1}^n e^{-\alpha r_i/N}}{\displaystyle\frac{n}{N}\left(\frac{1-e^{-\alpha}}{e^{\alpha/N}-1} \right)} \] \(n\)は正しい複合体の数（今回は1），\(r_i\)は（\(i\)番目の）正しい複合体の順位，\(\alpha\) はパラメータです．今回は \(\alpha=8.0\) としました．（参考：Truchon and Bayly, J Chem Inf Model, 2007.）
• AU-ROC: Area Under the Receiver Operating Characteristic Curve. 予測を上位から見ていって予測結果をカウントし，横軸に正しい結合相手で ないものの数を，縦軸に正しい結合相手の数をプロットしていったROC曲線の曲線下面積です．以下の式で計算されます． \[\mbox{AU-ROC}=1-\frac{\sum_{i=1}^n r_i}{n(N-n)}+\frac{n+1}{2(N-n)} \] \(n\)は正しい複合体の数（今回は1），\(r_i\)は（\(i\)番目の）正しい複合体の順位，\(N\)は全ての複合体の数（今回は120）です．
• AU-AC: Area Under the Accumulation Curve. ROC曲線の横軸を「全ての予測の数」に変えたものです．以下の式で計算されます． \[\mbox{AU-AC}=1-\frac{1}{nN}\sum_{i=1}^n r_i\] \(n\)は正しい複合体の数（今回は1），\(r_i\)は（\(i\)番目の）正しい複合体の順位，\(N\)は全ての複合体の数（今回は120）です．
• BEDROC: Bolzmann-Enhanced Discrimination ROC. RIEを0-1に正規化したような値で，近年Virtual Screening業界などでよく使われます． \[\mathrm{BEDROC}=\mathrm{RIE}\times\frac{\frac{n}{N}\sinh(\alpha/2)}{\cosh(\alpha/2)-\cosh(\alpha/2-\alpha n/N)}+\frac{1}{1-e^{\alpha(N-n)/N}}\] \(\alpha\) はRIEのパラメータと同一のものです．今回は\(\alpha=8.0\)としました．\(n=1, N=120\)です．
• EF: Enrichment Factor. よく使われる指標です． \[\mathrm{EF}=\frac{\mathrm{\#}(\mathrm{hits} | r_i \leq \chi N)}{\chi n}\] \(\chi\) はEFのパラメータで，上位\(\chi\)%に着目する，という意味になります．今回は\(\chi =0.2\)としました（\(\alpha=8.0\)とだいたい同じパラメータになる）．EFの最大値は\(1/\chi\)，ランダムのときは\(\lfloor \chi N\rfloor/\chi N\)となります．

● PPI Affinity BenchmarkによるPPI評価値と\(\Delta G_d\)の相関

PPI Affinity Benchmark (Kastritis et al., Protein Sci, 2011) を用いてPPI評価値 \(E\) とbinding affinity \(\Delta G_d\) の関係を検証しました．PPI Affinity Benchmarkの全144複合体に対してPPI評価値 \(E\) を求め，\(\Delta G_d\) とのPearson相関 係数を求めた結果を示します．

• ZRANKによるリランキング有り： \(\rho = 0.283\ \ \ (P\mathrm{-value}=5.82\times 10^{-4}<0.01)\)
• ZRANKによるリランキング無し： \(\rho = 0.228\ \ \ (P\mathrm{-value}=5.93\times 10^{-3}<0.01)\)

また，以下にそれぞれの散布図を示します．

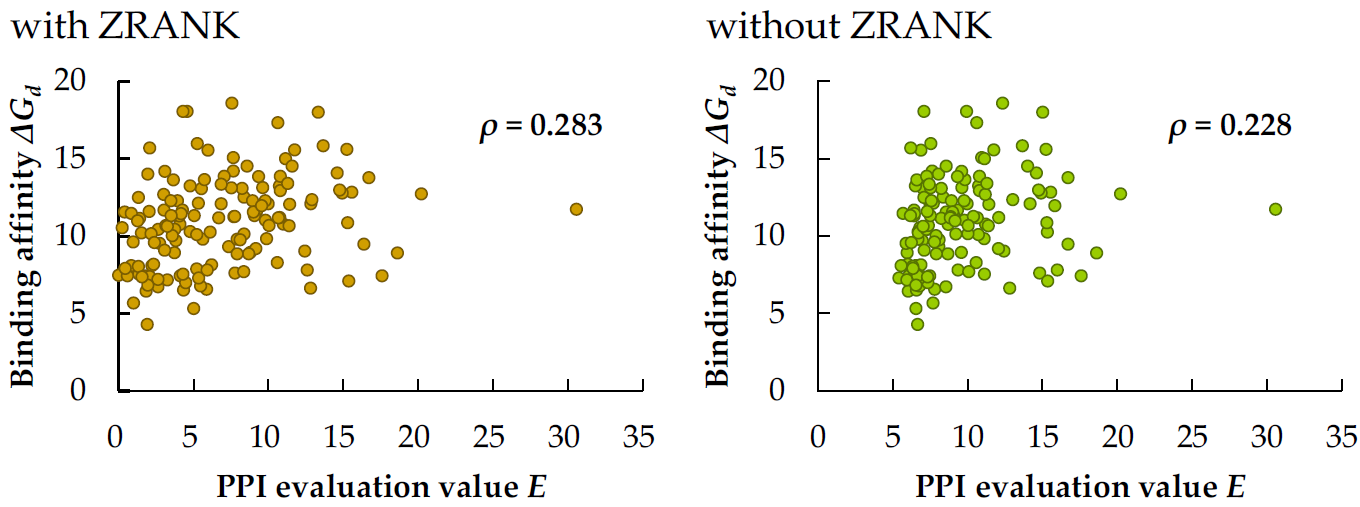図：PPI Affinity Benchmarkの144複合体のPPI評価値 \(E\) とAffinity \(\Delta G_d\)．各点がタンパク質複合体を表す．

● 参考文献

MEGADOCKグループ関連

• 本項で記述したPPI予測手法が記載された文献
  Ohue M, et al., Improvement of the Protein-Protein Docking Prediction by Introducing a Simple Hydrophobic Interaction Model: an Application to Interaction Pathway Analysis, Lecture Notes in Comput Sci, 7632: 178-187, 2012.
• MEGADOCKによるPPI予測の応用 (ヒトアポトーシスパスウェイ)
  Ohue M, et al., Highly Precise Protein-Protein Interaction Prediction Based on Consensus Between Template-Based and de Novo Docking Methods, BMC Proceedings, 7(Suppl 7): S6, 2013.
• MEGADOCKによるPPI予測の応用 (細菌走化性パスウェイ)
  Matsuzaki Y, et al., Protein-protein interaction network prediction by using rigid-body docking tools: application to bacterial chemotaxis, Protein Pept Lett, 21(8): 790-798, 2014.
• 候補構造のクラスタリングを用いたPPI予測
  Matsuzaki Y, et al., In silico screening of protein-protein interactions with all-to-all rigid docking and clustering: an application to pathway analysis, J Bioinform Comput Biol, 7(6): 991-1012, 2009.
• CAPRI Community-wide Assessment
  Fleishman SJ, et al., Community-Wide Assessment of Protein-Interface Modeling Suggests Improvements to Design Methodology, J Mol Biol, 414(2): 289-302, 2011.

その他の研究グループ

• Hexの形状項でbackground setからbinding partnerを識別
  Wass MN, et al., Towards the prediction of protein interaction partners using physical docking, Mol Syst Biol, 7: 469, 2011.
• MAXDoによるZLAB docking benchmark version 2.0の網羅的ドッキング
  Lopes A, et al., Protein-Protein Interactions in a Crowded Environment: An Analysis via Cross-Docking Simulations and Evolutionary Information, PLOS Comput Biol, 9(12): e1003369, 2013.
• SDOCKによるタンパク質複合体バーチャルスクリーニング
  Zhang C, et al., Discovery of binding proteins for a protein target using protein–protein docking-based virtual screening, Proteins, 82(10): 2472-2482, 2014.